- Inicio
- ⟩
- Matemáticas
- ⟩
- Herramienta matemática hecha en México se aplica en investigaciones internacionales
Herramienta matemática hecha en México se aplica en investigaciones internacionales
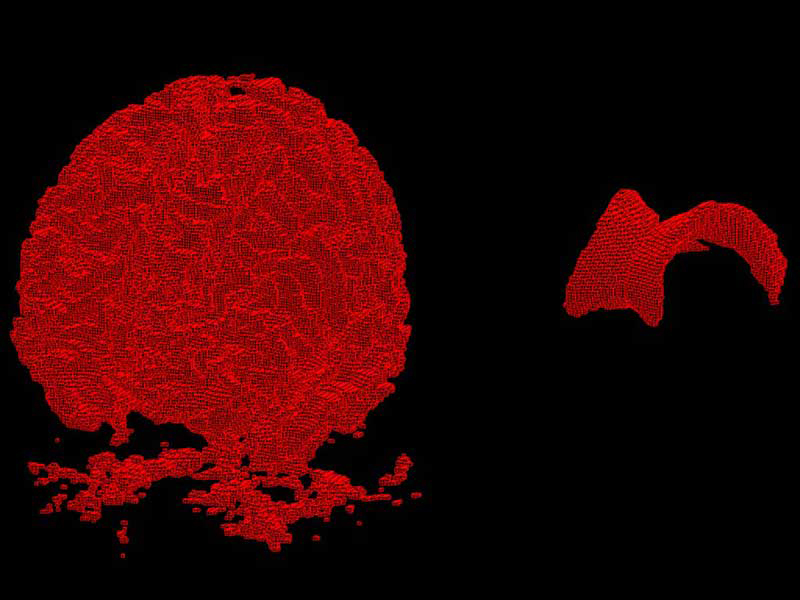
La compacidad discreta mide perímetros tortuosos. Foto: UAM-UNAM.
17-10-2011
Por María Luisa Santillán, DGCS-UNAM
El investigador mexicano Ernesto Bribiesca Correa, del Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas (IIMAS) de la UNAM, desarrolló la compacidad discreta, una herramienta matemática que sirve para conocer qué tan compacto es un objeto, a partir de su imagen digital, así como si aumenta o disminuye su tamaño.
De la información proporcionada por la compacidad discreta de un objeto es posible entender distintos procesos de su relación superficie-volumen. Lo relevante de esta aportación, que el investigador considera una sencilla ecuación, es que al saber qué tan compacto es un objeto en su estado normal, también es posible determinar si ha sufrido alguna alteración, es decir, si ha cambiado su forma, tamaño o estructura.
Entre otras aplicaciones, esta herramienta permite estudiar la compacidad de tumores cérvico-uterinos para conocer su tamaño, si se ha propagado la enfermedad hacia otros órganos, así como determinar su dispersión.
Imágenes que representan objetivos
La mayoría de las imágenes que usamos en la actualidad son digitales, ahora es común que al comprar una cámara fotográfica o un teléfono celular, además de la marca, nos preguntemos de qué resolución los queremos. Las imágenes digitales están compuestas por celdas, también conocidas como pixeles o pixels, las cuales podemos ver cuando ampliamos la imagen en nuestra computadora y notamos los cuadritos que la integran.
Para saber qué tan compacto es un objeto con la herramienta del doctor Bribiesca, primero se debe obtener la imagen digital del mismo y después medir el número de veces que se tocan los lados de las celdas que la conforman, es decir, el perímetro de contacto, gracias al cual es posible caracterizar los objetos o saber si sufren modificaciones.
Esta medida, que podría considerarse en un futuro como un estándar mundial para medir la compacidad de un objeto digital, es una aportación a la ciencia de las matemáticas a nivel mundial.
Hasta hace algunos años, gracias a la medida de la compacidad clásica (que tiene como característica importante la relación entre el perímetro y el área), conocer la compacidad de un objeto simple como un triángulo, un círculo, un cuadrado o un cubo era sencillo; sin embargo, el problema se presentaba cuando ésta quería calcularse en algún objeto complejo (con perímetros tortuosos), como un volcán, un tumor o el cerebro humano.
Con la ecuación de la compacidad discreta, el doctor Bribiesca Correa logró que el perímetro de un objeto ya no sea su referencia principal, sino su interior, por lo que apoyado con imágenes digitales de los objetos, cuenta el número de lados que se tocan entre sí las celdas. Así, un objeto es poco compacto entre menos contacto haya entre sus celdas y es más compacto a un mayor contacto entre ellas.
Un estándar mundial de orginen nacional
En entrevista, el doctor Bribiesca comentó que ha trabajado en el desarrollo de la compacidad discreta desde hace aproximadamente 12 años y, por ser una herramienta matemática de fácil aplicación, expertos de distintas áreas la han utilizado para adaptarla a diversos campos del conocimiento.
Tal es el caso del trabajo que realiza en colaboración con investigadores de la Universidad de Leipzig, en Alemania. El grupo integrado por médicos, oncólogos y ginecólogos ha utilizado la compacidad discreta para clasificar tumores cérvico uterinos: “Cuando el tumor es muy compacto está muy redondeado, pero si el tumor está muy disperso, tiene ramificaciones. Esto es importante porque nos indica cómo se está propagando el tumor y nuestra medida se vuelve muy sensible a estos cambios”, indica el investigador.
Cabe destacar que esta herramienta matemática es sólo un parámetro, un auxiliar más para el experto, a partir de la cual él puede conocer la estructura de los tumores y, en determinado momento, tomar decisiones sobre cómo tratarlos.
Bribiesca Correa y el grupo de investigadores alemanes están por publicar un artículo en el que agregaron un parámetro importante a su cálculo que consiste en conocer qué tan poroso es un objeto, ya que los tumores, con frecuencia, presentan huecos y esta nueva característica enriquecería el conocimiento sobre estos.
“La gente de Alemania encontró que había muchas ventajas de utilizar la medida que propusimos aquí en el IIMAS y la compararon con la medida clásica. Esta comparación la publicaron en una revista internacional de calidad, donde mencionan que han tenido mucho éxito con la compacidad discreta, por lo que la proponen para que sea el nuevo estándar mundial para clasificar los tumores”, comentó.
Desde imágenes cerebrales hasta zonas electorales
En México, Ernesto Bribiesca Correa colaboró con un grupo de investigadores de la Universidad Autónoma Metropolitana-Iztapalapa (UAM-I) para clasificar imágenes cerebrales. Con la clasificación obtenida, a través de la compacidad discreta se ha visto que la superficie envolvente de una estructura cerebral cambia con relación a su volumen cuando el órgano ha sido afectado por algunos padecimientos, tal como la enfermedad de Alzheimer.
Asimismo, el instrumento creado por el doctor Bribiesca se utiliza en Dinamarca para calcular la forma y compacidad de la vejiga urinaria en adultos mayores. En Francia, la herramienta matemática se utilizó para clasificar tumores cuyas superficies están muy corrugadas. En Canadá, a su vez, usan esta ecuación para medir la compacidad de los suelos.
Además, en nuestro país, y en un ámbito totalmente distinto, la compacidad discreta fue utilizada para clasificar las zonas electorales, pues se espera que a futuro éstas tengan una densidad de votantes similar por cuestiones de estadística y accesibilidad.
Finalmente, el investigador mexicano comenta que aunque la ecuación prácticamente está concluida, otros grupos de investigación lo han invitado a trabajar para nuevas aplicaciones, para realizar una mejora de la ecuación o para relacionarla con otros parámetros.
Publicaciones relacionadas

Ciencia y tecnología hecha por jóvenes para resolver los grandes retos de México

Marcos Moshinsky, gran expositor de la teoría matemática de la simetría en la naturaleza

Especial México 68. Las Olimpiadas entre la agitación social