Qué partido ganará las próximas elecciones en México, según la estadística bayesiana

El objeto de estudio de la estadística son los fenómenos aleatorios, es decir, aquellos que no se pueden predecir con certeza. Existen varias escuelas de la estadística, aunque las dos que dominan en la actualidad son la frecuentista y la bayesiana.

La diferencia fundamental entre estas dos escuelas es la interpretación de la probabilidad que cada una utiliza. Por ejemplo, la frecuentista se relaciona más con la experimentación: si un evento se repite un gran número de veces bajo condiciones similares, a partir de esa experiencia se puede definir qué tan probable es que ocurra en el futuro. En este tipo de estadística lo más importante son los datos.

Por su parte, la estadística bayesiana hace uso de la interpretación subjetiva de la probabilidad. De acuerdo con el doctor Eduardo Gutiérrez Peña, del Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas de la UNAM, desde el punto de vista bayesiano, la probabilidad se ve como una medida del grado de información que uno tiene sobre la ocurrencia de un evento.

Por ejemplo, ante la pregunta ¿qué partido político ganará las elecciones que se llevarán a cabo este 2018 en México? Aunque la respuesta no la tenemos en estos momentos (se sabrá hasta poco después del día de las elecciones), sí podemos asignar una probabilidad y pensar qué tan probable es que gane un partido u otro en función de la información que tenemos ahora sobre esos eventos.

“Pero es una apreciación subjetiva; lo que yo pueda pensar sobre esto difiere probablemente mucho de lo que piensa un analista político que es experto en el tema. Él, con la información a su disposición, tal vez juzgue que no es tan probable que gane cierto partido, mientras que yo, con la información que tengo, no lo sé, pero juzgo que sí es probable. Esas diferencias en las probabilidades que vamos a asignar se deben a distintos estados de información”, destacó.

Por lo tanto, desde el punto de vista bayesiano la asignación de la probabilidad se hace de manera subjetiva, es decir, la asigna la persona en función de todo lo que sabe. La estadística frecuentista, por el contrario, pretende ser objetiva, en otras palabras, no está sujeta a la información con la que cuenta la persona, sino que establece probabilidades de manera empírica.

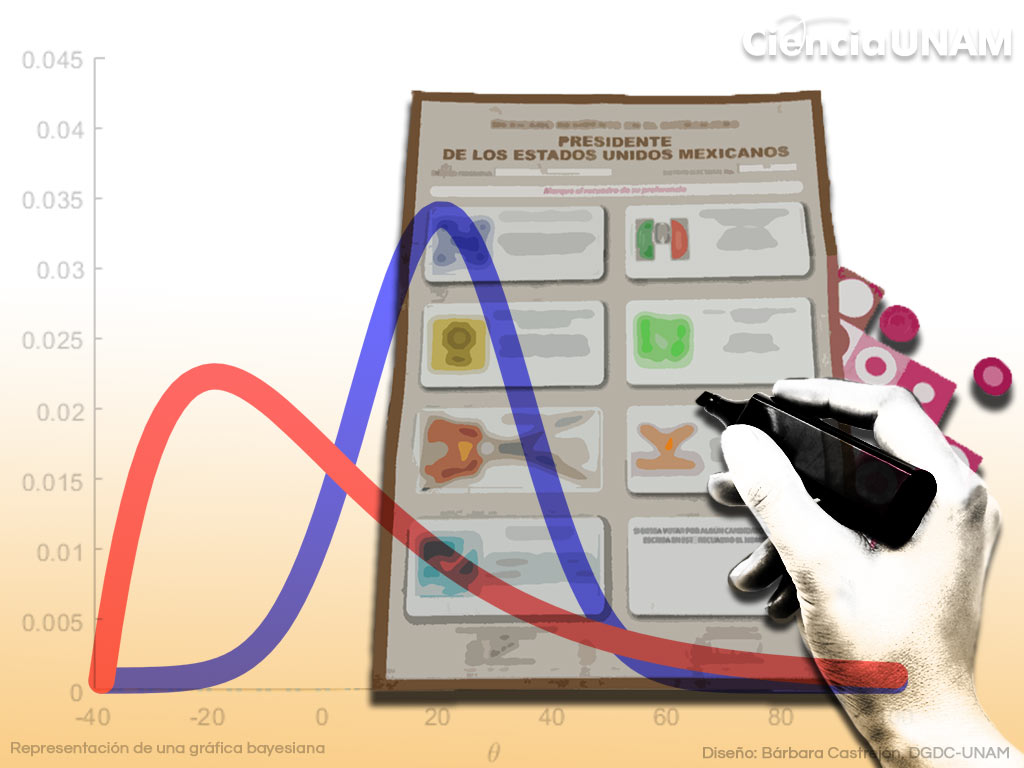
El doctor Gutiérrez Peña explicó que la interpretación frecuentista de la probabilidad puede presentar dificultades para asignar probabilidades a cierto tipo de eventos, por ejemplo, como el antes mencionado.

“Las próximas elecciones no son parecidas a ninguna otra, cada una es distinta. El argumento frecuentista depende de poder suponer que el evento de interés se puede repetir muchas veces y en condiciones similares, y esto no es así en este caso. Por eso este problema no se podría resolver tan fácilmente con la interpretación frecuentista de la probabilidad, porque no tenemos datos para evaluarlo de esa manera”, dijo.

Aplicación en distintas áreas

Cualquier área del conocimiento puede emplear la estadística bayesiana, específicamente en problemas científicos donde sea necesario cuantificar la incertidumbre, tales como problemas de pronóstico financieros o meteorológicos, en estudios de geofísica, ciencias sociales, sistemas biológicos, etcétera.

En el área de ciencias de la salud el enfoque bayesiano ha sido particularmente importante, sobre todo en el análisis de ensayos clínicos que determinan la efectividad de nuevos tratamientos para combatir enfermedades.

Al respecto, el doctor Gutiérrez Peña detalló que “en este contexto, por lo general, se cuenta con muy pocos datos, así que la posibilidad de combinar la información de los expertos con la, muchas veces, escasa evidencia muestral, es crucial. En este sentido, los métodos bayesianos también permiten la combinación, o meta análisis, de la evidencia de distintos estudios, con el fin de producir inferencias más confiables sobre las hipótesis de interés”.

• La estadística bayesiana surgió aproximadamente hace 250 años a partir de la publicación póstuma del Teorema de Bayes en 1763.

El investigador señaló que una de las aplicaciones más cotidianas del Teorema de Bayes, más allá de las aplicaciones científicas de la estadística bayesiana, está en los problemas de clasificación, por ejemplo, en los filtros de spam (correo basura) que están activos en nuestro correo electrónico. El teorema se utiliza para decidir si un correo se clasifica como basura o no.

Además, de acuerdo con la información que proporciona el usuario al reclasificar manualmente los mensajes más clasificados, se va incrementando la probabilidad de que los siguientes mensajes de spam sean clasificados como tales y que los que son genuinos terminen en el buzón normal. En otras palabras, el algoritmo “aprende” gracias al Teorema de Bayes.

Probabilidad e incertidumbre

Siempre que haya un problema donde se requiera la estadística, la estadística bayesiana va a ser una alternativa, pues cualquier problema que se pueda resolver desde el punto de vista frecuentista, también se puede solucionar desde el punto de vista bayesiano, con la ventaja de que si es necesario se puede incorporar la información adicional con la que cuente el experto.

Sin embargo, la estadística bayesiana ha sido controvertida, sobre todo, porque como lo explica el doctor Gutiérrez Peña, “se supone que en cierto sentido la ciencia tiene que ser objetiva y eso de alguna manera es lo contrario a lo que postula la estadística bayesiana, que enfatiza en que la interpretación de la probabilidad depende del grado de conocimiento de cada persona y, por lo tanto, es subjetiva”.

Otro tema que está ligado a la estadística bayesiana es el de la teoría de la decisión en ambiente de incertidumbre. Algunos problemas que tal vez no son evidentemente estadísticos, de alguna manera se podrían plantear como problemas de decisión y tienen que ver con manejo de información.

Por ejemplo, si un inversionista tiene que decidir cómo distribuir sus recursos en distintos fondos de inversión o en distintas opciones, ese problema implica incertidumbre, porque obviamente no sabe cuál es el que va a darle mejores rendimientos; no lo sabe con certeza, pero sí puede tener información que le diga que lo más probable es que uno de ellos le dé buenos rendimientos y los otros menos. En cualquier caso, antes de tomar una decisión tiene que evaluar las distintas opciones dependiendo de cuáles tienen más riesgo, cuáles son más probables que suban, etcétera.

Para producir procedimientos adecuados que permitan tomar este tipo de decisiones es que existe la teoría de la decisión, la cual está relacionada con la estadística bayesiana porque proporciona una forma de justificarla y, en particular, de justificar la interpretación subjetiva de la probabilidad, concluyó.